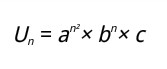Barisan aritmetika yang bedanya membentuk barisan aritmetika juga.
(bedanya tidak konstan tapi teratur).
Bentuk barisan aritmetika tingkat dua
Dengan rumus tersebut kita dapatkan
sehingga
dan
Jadi, rumus suku ke-n pada barisan aritmetika tingkat dua adalah
- Barisan Aritmetika Tingkat Dua
Bentuk barisan aritmetika tingkat dua
Bentuk rumus suku ke-n
sehingga
dan
Jadi, rumus suku ke-n pada barisan aritmetika tingkat dua adalah
dengan a, b, dan c didapat dari
Bentuk barisan aritmetika tingkat tiga
Bentuk rumus suku ke-n
Dengan teknik seperti pada barisan aritmetika tingkat dua,
a, b, c, dan d didapat dari
Demikian pula teknik untuk menentukan rumus barisan aritmetika dengan tingkat yang lebih tinggi.
2. Jika 300 merupakan salah satu suku pada barisan Un = 2n² + 5n + k, tentukan bilangan bulat positif terkecil yang memenuhi k !
Pembahasan
1.
1 = 2a
a = 1/2
2 = 3a + b
2 = 3/2 + b
b = 1/2
1 = a + b + c
1 = 1/2 + 1/2 + c
c = 0
Un = n²/2 + n/2
U25 = 625/2 + 25/2
U25 = 650/2
U25 = 325
Jadi, suku yang ke-25 adalah 325.
2. 300 = 2n² + 5n + k
2n² + 5n + k - 300 = 0
terbentuk persamaan kuadrat dengan
a = 2
b = 5
c = k - 300
nilai n pasti bilangan bulat, berarti deskriminan harus bilangan kuadrat (agar bisa ditarik akar)
b² - 4ac
= 25 - 4(2)(k - 300)
= 25 - 8(k - 300)
= 25 - 8k + 2400
= 2425 - 8k
dari sini kita coba-coba bilangan bulat positif untuk k, dimulai dari 1
bilangan pertama yang memenuhi adalah 3, kita coba substitusikan
n = -b ± √D
2a
= -5 ± √2401
4
= 11 atau -13,5
(kita ambil n = 11 saja)
Karena k = 3 menghasilkan n bulat positif, berarti bilangan bulat positif terkecil yang memenuhi k adalah 3.
- Barisan Aritmetika Tingkat Tiga
Bentuk barisan aritmetika tingkat tiga
Bentuk rumus suku ke-n
Dengan teknik seperti pada barisan aritmetika tingkat dua,
a, b, c, dan d didapat dari
Demikian pula teknik untuk menentukan rumus barisan aritmetika dengan tingkat yang lebih tinggi.
- Contoh soal
2. Jika 300 merupakan salah satu suku pada barisan Un = 2n² + 5n + k, tentukan bilangan bulat positif terkecil yang memenuhi k !
Pembahasan
1.
Karena beda sudah konstan setelah terbentuk tiga barisan, maka ini merupakan barisan aritmetika tingkat dua.
a = 1/2
2 = 3a + b
2 = 3/2 + b
b = 1/2
1 = a + b + c
1 = 1/2 + 1/2 + c
c = 0
Un = n²/2 + n/2
U25 = 625/2 + 25/2
U25 = 650/2
U25 = 325
Jadi, suku yang ke-25 adalah 325.
2. 300 = 2n² + 5n + k
2n² + 5n + k - 300 = 0
terbentuk persamaan kuadrat dengan
a = 2
b = 5
c = k - 300
nilai n pasti bilangan bulat, berarti deskriminan harus bilangan kuadrat (agar bisa ditarik akar)
b² - 4ac
= 25 - 4(2)(k - 300)
= 25 - 8(k - 300)
= 25 - 8k + 2400
= 2425 - 8k
dari sini kita coba-coba bilangan bulat positif untuk k, dimulai dari 1
bilangan pertama yang memenuhi adalah 3, kita coba substitusikan
n = -b ± √D
2a
= -5 ± √2401
4
= 11 atau -13,5
(kita ambil n = 11 saja)
Karena k = 3 menghasilkan n bulat positif, berarti bilangan bulat positif terkecil yang memenuhi k adalah 3.