(rasionya tidak konstan tapi teratur).
- Barisan Geometri Tingkat Dua
Bentuk barisan geometri tingkat dua
berarti
sehingga
dan
Jadi, rumus barisan geometri tingkat dua ialah
dengan a, b, dan c didapat dari
- Barisan Geometri Tingkat Tiga
Rasio baru konstan setelah terbentuk empat barisan.
Bentuk barisan geometri tingkat tiga
Bentuk rumus mencari suku ke-n
Dengan cara yang sama seperti pada barisan geometri tingkat dua
a, b, c, dan d didapat dari
Begitu pula untuk mencari rumus suku ke-n pada barisan geometri bertingkat yang lebih tinggi.
Bentuk rumus mencari suku ke-n
Dengan cara yang sama seperti pada barisan geometri tingkat dua
a, b, c, dan d didapat dari
Begitu pula untuk mencari rumus suku ke-n pada barisan geometri bertingkat yang lebih tinggi.
- Contoh soal
Tentukan suku ke-7 pada barisan 1/3 , 1 , 12 , 576 , ... !
PembahasanKarena rasio sudah konstan ketika terbentuk 3 barisan, berarti barisan ini merupakan barisan geometri tingkat dua
a² = 4
a = 2 atau -2
a³b = 3
8b = 3 atau -8b = 3
b = 3/8 atau -3/8
abc = 1/3
2(3/8)c = 1/3 atau -2(-3/8)c = 1/3
jadinya sama-sama
(3/4)c = 1/3
c = 4/9
berarti rumusnya
yang ditanya adalah suku ke-7
Jadi, suku yang ke-7 adalah 2^30 × 3^5
(Rumus dengan a = -2 dan b = -3/8 juga menghasilkan hasil yang sama)

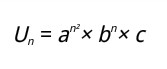











S10 dari 1/2 1/6 1/12 1/20?
BalasHapusKomentar ini telah dihapus oleh pengarang.
BalasHapusPola barisan geometri tersebut dengan ratio yg tidak konstan
BalasHapusBisa dinyatakan sebagai barisan geometri bertingkat
Jika Anda mencari rumus untuk Jumlah barisan geometri bertingkat, rumusnya akan berbeda karena ratio tidak konstan, dan Anda perlu mencari pola ratio tingkat pertama, kedua, dan seterusnya hingga menemukan ratio yang konstan.
hingga kini belom ada rumus "barisan geometri bertingkat yang baku" dalam matematika,
Tapi u pembahasan lebih lanjut perhitungan bisa menggunakan metode fungsi gamma (invers faktorial)